Machine Learning
De lo simple a lo sofisticado: Predicción del porcentaje de proteína del haba de soja
03 Jul

Autor: Marco Catroppa
La necesidad de estimar—de forma fiable y anticipada—métricas de productos asociadas a procesos industriales es uno de los retos más candentes en el ámbito científico-tecnológico actual. La tendencia creciente a introducir Gemelos Digitales en entornos industriales ha transformado profundamente la forma en que se controlan, optimizan y comprenden dichos procesos. Más allá de una simple digitalización, un Gemelo Digital implica la capacidad de predecir en tiempo real variables críticas del sistema, habilitando respuestas automáticas y decisiones informadas sin necesidad de intervención externa ni demoras asociadas a análisis offline.
En este contexto, con respecto al proceso industrial de extracción de proteína de haba de soja, se emprendió un trabajo de modelización predictiva centrado en la estimación de la concentración de proteína, clave para la calidad del producto final.
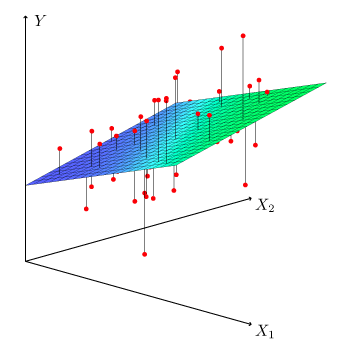
El primer paso consistió en establecer una línea base (baseline) mediante un modelo de Regresión Lineal Múltiple (RLM), que permitió identificar relaciones directas entre variables de proceso y la concentración proteica. Aunque el modelo ofrecía interpretabilidad y una buena aproximación inicial, el análisis residual reveló patrones indeseados como heterocedasticidad y autocorrelación, lo que indicaba una posible ineficiencia de las estimaciones. Estos problemas, típicos en contextos industriales donde las condiciones operativas no son perfectamente controladas, pusieron de manifiesto la necesidad de modelos más robustos.
En este artículo analizamos los beneficios y riesgos de ambas alternativas, con el objetivo de ofrecer una visión estratégica y técnica que ayude a tomar decisiones fundamentadas, especialmente en contextos donde la privacidad, la trazabilidad del dato y la soberanía tecnológica son críticas.
Para subsanar estas limitaciones, se adoptó una estrategia basada en la Regresión Generalizada de Mínimos Cuadrados (GLS), que permite modelar explícitamente la estructura de varianza y dependencia entre observaciones. Este ajuste mejoró significativamente el comportamiento estadístico del modelo: los residuos se distribuyeron de forma más uniforme y el coeficiente de determinación aumentó. Más allá de la mejora técnica, este modelo consolidó una herramienta de estimación confiable que, manteniéndose en el marco lineal, respetaba la restricción de aplicabilidad operativa.
Superada esta fase, y conscientes de que las relaciones entre variables del proceso no siempre son lineales ni aditivas, se introdujeron técnicas de machine learning más sofisticadas. En particular, se entrenó un modelo Random Forest sobre el mismo conjunto de variables medibles en tiempo real. Su naturaleza no paramétrica permitió capturar interacciones complejas y patrones no lineales que los modelos lineales no lograban representar.
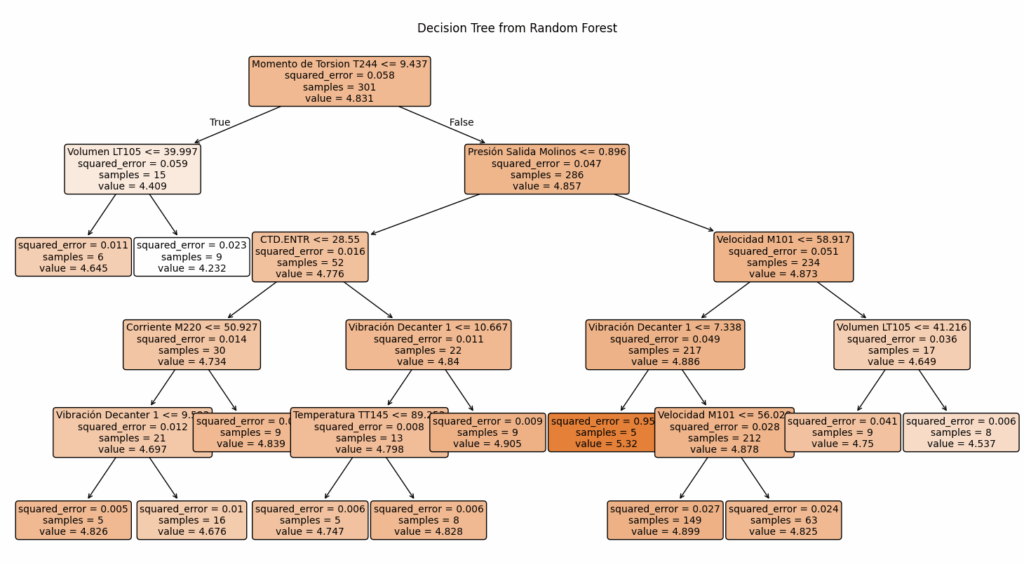
Durante este proceso, el modelo Random Forest también arrojó luz sobre la relevancia de las distintas variables de entrada. La estimación de importancia evidenció redundancias entre ciertas variables. Esto motivó la exploración de técnicas de reducción de dimensionalidad no lineales, en particular el Análisis de Componentes Principales con Kernel (Kernel PCA). Al transformar los datos a un espacio de características donde las relaciones entre variables se volviesen linealmente separables, se logró identificar estructuras latentes del proceso, mejorando no solo la comprensión del mismo, sino también la calidad del modelo.
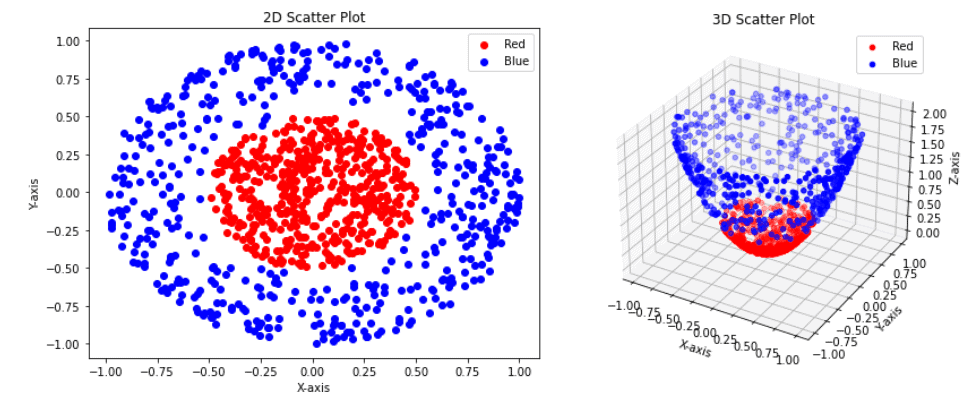
A través de esta técnica se identificaron combinaciones de variables que concentraban la mayor parte de la variabilidad informativa del sistema. Incorporar estas componentes al modelo Random Forest no solo permitió una mejora en la precisión, sino que condujo a un modelo más parsimonioso y robusto. Finalmente, al seleccionar un subconjunto óptimo de variables originales —guiados por la estructura descubierta con el Kernel PCA— se construyó una versión optimizada del modelo Random Forest que alcanzó el mejor desempeño registrado hasta la fecha, con menor complejidad y mayor capacidad de generalización.
Conclusión
El desarrollo de este sistema predictivo ejemplifica cómo una metodología iterativa, fundamentada en el conocimiento del proceso y en una visión crítica del comportamiento de los modelos, permite construir soluciones eficaces para entornos industriales reales. Lejos de buscar sofisticación por sí misma, cada técnica aplicada respondió a una necesidad concreta: mejorar la robustez, capturar no linealidades, reducir redundancia o facilitar la integración operativa.
La transición desde modelos lineales hasta algoritmos más complejos no fue abrupta, sino guiada por la evidencia técnica y por una lógica de mejora continua. Esta combinación de enfoques estadísticos clásicos con herramientas modernas de machine learning y análisis de características permite no solo mejorar la precisión, sino también acercar la analítica avanzada al lenguaje operativo de planta.
Artículos relacionados
Email: info@foqum.io
Teléfono: +34 675 481 701
C. de Agustín Durán, 24, Local bajo izquierda, 28028 Madrid.